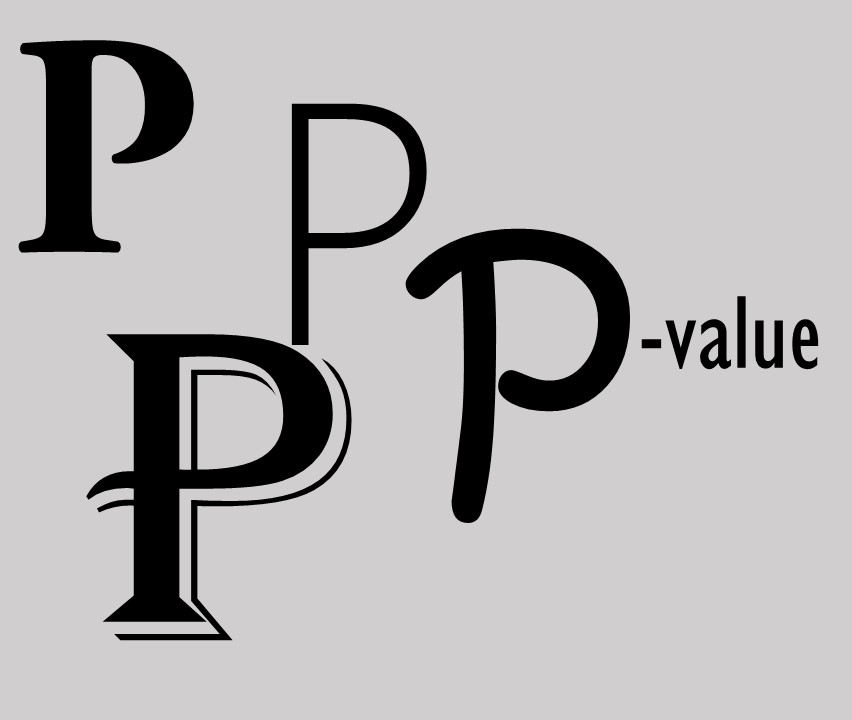Invariance analyses in large-scale studies
This report sets out to identify and apply novel procedures to evaluate model fit across a large number of groups, or novel scaling models that are more likely to pass common model fit criteria.
Testing Small Variance Priors Using Prior-Posterior Predictive P-values
Muthen and Asparouhov (2012) propose to evaluate model fit in structural equation models based on approximate (using small variance priors) instead of exact equality of (combinations of) parameters to zero. This is an important development that adequately addresses Cohen’s (1994) “The earth is round (p < .05)”, which stresses that point null-hypotheses are so precise that small and irrelevant differences from the null-hypothesis may lead to their rejection.
People management: developing and testing a measurement scale
In this study we conceptualize people management and develop a multidimensional scale to measure it from the perspectives of both employees and line managers.
The relationship between tics, OC, ADHD and autism symptoms
Gilles de la Tourette’s syndrome (GTS) is a disorder in which obsessive-compulsive (OC), Attention Deficit Hyperactivity Disorder (ADHD) and autism symptoms occur in up to 60% of patients, suggesting shared etiology.
The Stability of Problem Behavior Across the Preschool Years: An Empirical Approach in the General Population
This study examined the stability of internalizing and externalizing problems from age 1.5 to 6 years, while taking into account developmental changes in the presentation of problems. The study comprised a population-based cohort of 7,206 children (50.4 % boys).
Measurement Invariance (book)
Multi-item surveys are frequently used to study scores on latent factors, like human values, attitudes and behavior. Such studies often include a comparison, between specific groups of individuals, either at one or multiple points in time.
Experience of traumatic events disrupts measurement invariance of a posttraumatic stress scale
Studies that include multiple assessments of a particular instrument within the same population are based on the presumption that this instrument measures the same construct over time. But what if the meaning of the construct changes over time due to one’s experiences?
Promotion of students’ mastery goal orientations: does TARGET work?
Achievement goal orientations are important for students’ ongoing motivation. Students with a mastery goal orientation show the most advantageous achievement and motivational patterns. Much research has been conducted to identify classroom structures which promote students’ mastery goal orientation.
Measurement invariance of the Illness Invalidation Inventory
The Illness Invalidation Inventory (3*I) assesses patients’ perception of responses of others that are perceived as denying, lecturing, not supporting and not acknowledging the condition of the patient. It includes two factors: ‘discounting’ and ‘lack of understanding’.
Using the Youth Self-Report internalizing syndrome scales among immigrant adolescents
Although the Youth Self-Report (YSR) has been used in many studies throughout the world, little is known about the equivalence of the factor structure of this instrument for immigrant adolescents.
The Satisfaction With Life Scale: Measurement invariance across immigrant groups
The current study examined measurement invariance of the Satisfaction With Life Scale (SWLS; Diener, Emmons, Larsen, & Griffin, 1985) across three immigrant groups, namely, immigrants from the Former Soviet Union (FSU) in Israel, Turkish-Bulgarians, and Turkish-Germans. The results demonstrate measurement invariance of the SWLS across groups.