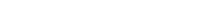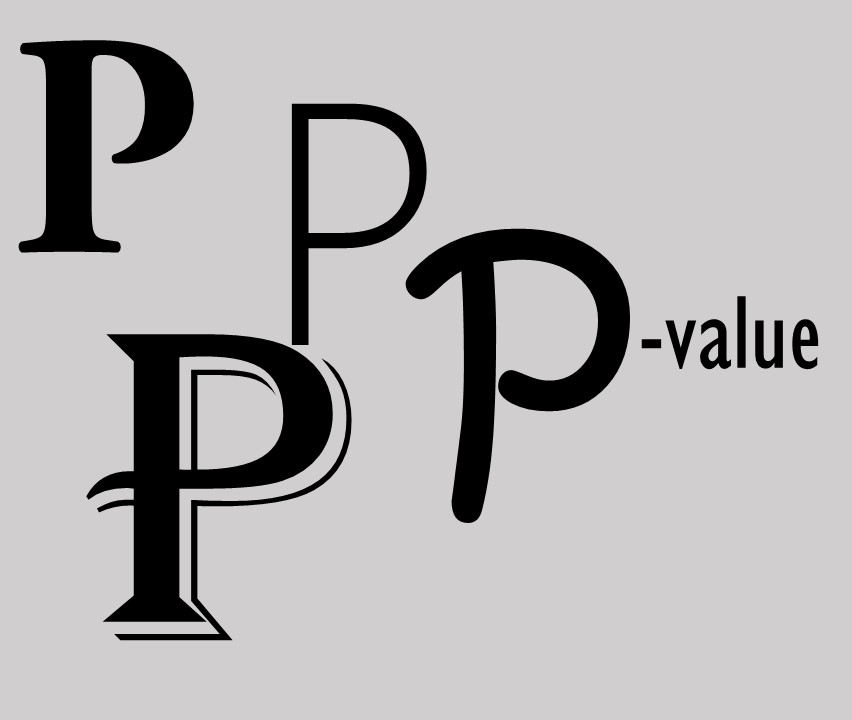Small Sample Size Solutions: A Guide for Applied Researchers and Practitioners.
This unique resource provides guidelines and tools for implementing solutions to issues that arise in small sample research, illustrating statistical methods that allow researchers to apply the optimal statistical model for their research question when the sample is too small.
Quantifying the informational value of classification images
In this article, we propose a novel metric, infoVal, which assesses informational value relative to a re-sampled random distribution and can be interpreted like a z score.
Dealing with imperfect elicitation results
We provide an overview of the solutions we used for dealing with imperfect elicitation results, so that others can benefit from our experience. We present information about the nature of our project, the reasons for the imperfect results, and how...
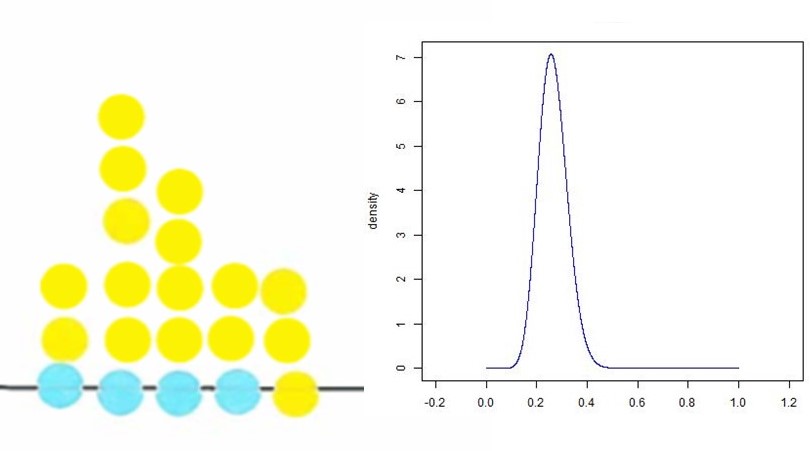
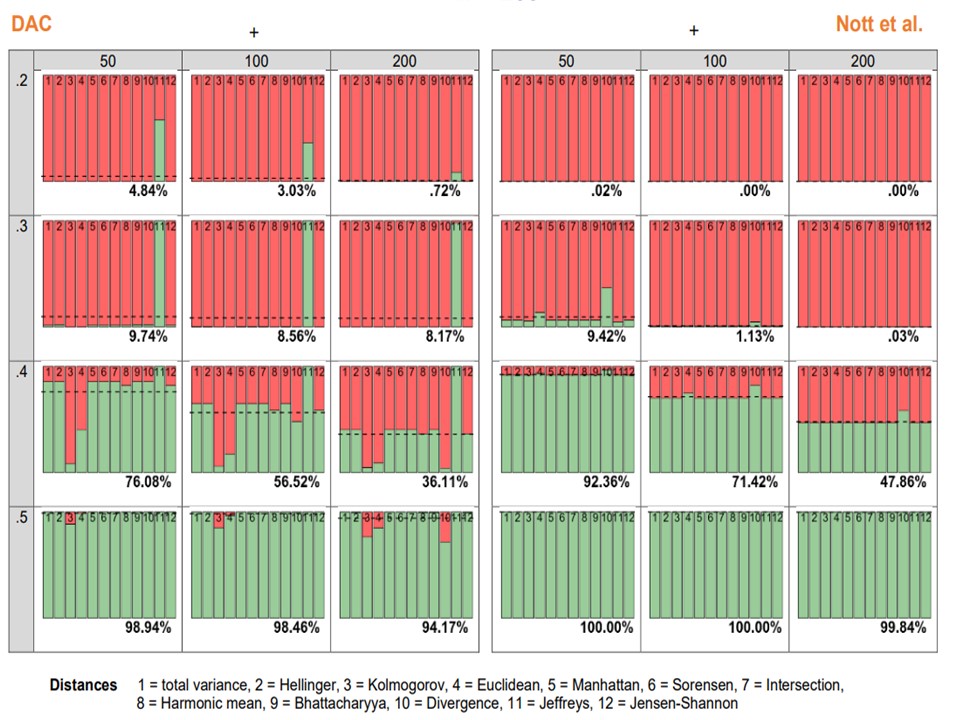
Choice of Distance Measure Influences the Detection of Prior-Data Conflict
The present paper contrasts two related criteria for the evaluation of prior-data conflict: the Data Agreement Criterion (DAC; Bousquet, 2008) and the criterion of Nott et al. (2016). We investigated how the choice of a specific distance measure influences the...
Testing Small Variance Priors Using Prior-Posterior Predictive P-values
Muthen and Asparouhov (2012) propose to evaluate model fit in structural equation models based on approximate (using small variance priors) instead of exact equality of (combinations of) parameters to zero. This is an important development that adequately addresses Cohen’s (1994)...
A comparison of the single, conditional and person-specific standard error of measurement
Tests based on the Classical Test Theory often use the standard error of measurement (SEm) as an expression of (un)certainty in test results. Although by convention a single SEm is calculated for all examinees, it is also possible to (1)...
Using the Data Agreement Criterion to Rank Experts’ Beliefs
We evaluated priors based on expert knowledge by extending an existing prior-data (dis)agreement measure, the Data Agreement Criterion, and compare this approach to using Bayes factors to assess prior specification.
Measurement Invariance (book)
Multi-item surveys are frequently used to study scores on latent factors, like human values, attitudes and behavior. Such studies often include a comparison, between specific groups of individuals, either at one or multiple points in time.
“Is the Hypothesis Correct” or “Is it Not”: Bayesian Evaluation of One Informative Hypothesis for ANOVA
Researchers in the behavioral and social sciences often have one informative hypothesis with respect to the state of affairs in the population from which they sampled their data. The question they would like an answer to is “Is the Hypothesis...
Bayesian Evaluation of Inequality-Constrained Hypotheses in SEM Models using Mplus
Researchers in the behavioral and social sciences often have expectations that can be expressed in the form of inequality constraints among the parameters of a structural equation model resulting in an informative hypothesis. The questions they would like an answer...
One Size Does Not Fit All: proposal for a prior-adapted BIC
This paper presents a refinement of the Bayesian Information Criterion (BIC). While the original BIC selects models on the basis of complexity and fit, the so-called prior-adapted BIC allows us to choose among statistical models that differ on three scores:...
A prior predictive loss function for the evaluation of inequality constrained hypotheses
In many types of statistical modeling, inequality constraints are imposed between the parameters of interest. As we will show in this paper, the DIC (i.e., posterior Deviance Information Criterium as proposed as a Bayesian model selection tool by Spiegelhalter, Best,...